Does A Triangle Equal 180

Historic period xiv to eighteen

Published 2002 Revised 2012

1. Introduction

Practise the angles of a triangle add together upwardly to 180 degrees or $\pi$ radians? The respond is 'sometimes yeah, sometimes no'. Is this an important question? Yep, because it leads to an understanding that there are different geometries based on different axioms or 'rules of the game of geometry'. Is information technology a meaningful question? Well no, at least not until we take agreed on the meaning of the words 'bending' and 'triangle', not until we know the rules of the game. In this commodity we briefly discuss the underlying axioms and give a simple proof that the sum of the angles of a triangle on the surface of a unit sphere is non equal to $\pi$ but to $\pi$ plus the area of the triangle. We shall use the fact that the surface area of the surface of a unit sphere is $iv\pi$.

2. The Big Theorem

Earlier nosotros tin can say what a triangle is we demand to agree on what we mean past points and lines. We are working on spherical geometry (literally geometry on the surface of a sphere). In this geometry the space is the surface of the sphere; the points are points on that surface, and the line of shortest distance between two points is the great circle containing the two points. A great circle (like the Equator) cuts the sphere into two equal hemispheres. This geometry has obvious applications to distances between places and air-routes on the Earth.

Rotating sphere showing swell circle

The angle between two bully circles at a betoken P is the Euclidean angle between the directions of the circles (or strictly between the tangents to the circles at P). This presents no difficulty in navigation on the World because at any given indicate nosotros think of the angle between two directions equally if the Earth were apartment at that point.

A lune is a office of the surface of the sphere divisional by two dandy circles which run across at antipodal points. We outset consider the area of a lune and and then innovate another peachy circle that splits the lune into triangles.

Rotating sphere showing 4 lunes

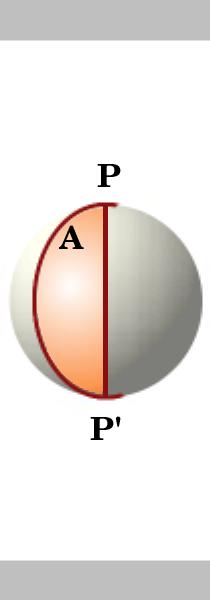Lemma.

The area of a lune on a circumvolve of unit radius is twice its angle, that is if the angle of the lune is A then its area is 2A. Two great circles intersecting at antipodal points P and P' split up the sphere into four lunes. The area of the surface of a unit sphere is $4\pi$.

The areas of the lunes are proportional to their angles at P so the surface area of a lune with bending A is

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Exercise i.

What are the areas of the other 3 lunes? Do your iv areas add together up to $iv\pi$?

Check your answers here .

The sides of a triangle ABC are segments of three cracking circles which actually cut the surface of the sphere into 8 spherical triangles. Between the 2 dandy circles through the point A in that location are four angles. We label the angle inside triangle ABC as angle A, and similarly the other angles of triangle ABC as angle B and angle C.

Rotating sphere showing eight triangles

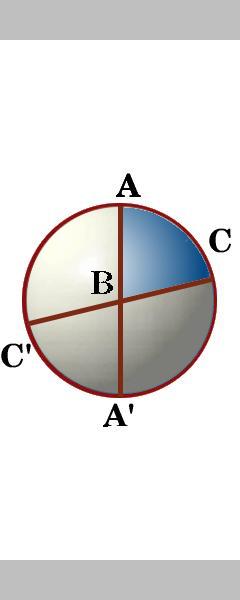Practice ii

Rotating the sphere tin you name the eight triangles and say whether any of them have the same area? Check your answers hither .

Theorem.

Consider a spherical triangle ABC on the unit sphere with angles A, B and C. Then the area of triangle ABC is

A + B + C - $\pi$.

The diagram shows a view looking down on the hemisphere which has the line through Air-conditioning as its purlieus. The regions marked Area one and Area 3 are lunes with angles A and C respectively. Consider the lunes through B and B'. Triangle ABC is congruent to triangle A'B'C' so the bow-necktie shaped shaded surface area, marked Area 2, which is the sum of the areas of the triangles ABC and A'BC', is equal to the area of the lune with angle B, that is equal to 2B.

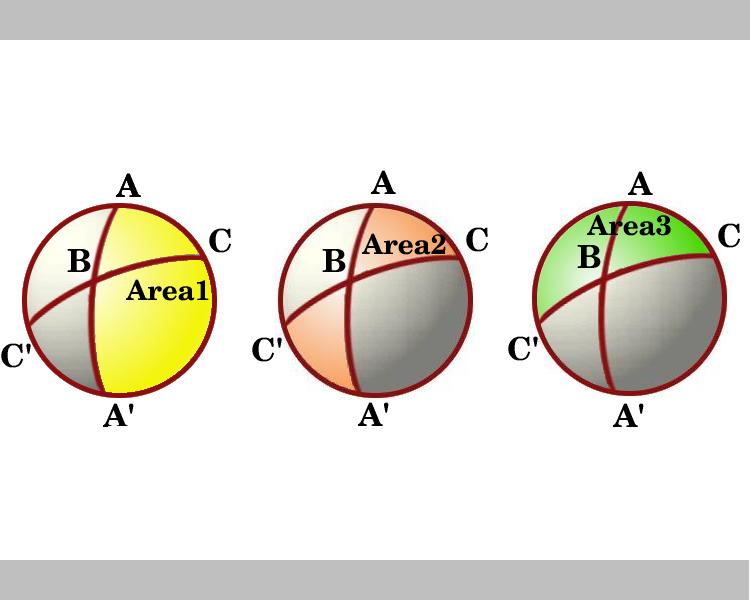
So in the diagram we run into the areas of three lunes and, using the lemma, these are:

Surface area 1 = 2A
Area 2 = 2B
Area 3 = 2C

In adding upwards these 3 areas we include the area of the triangle ABC iii times. Hence

Area 1 + Area 2 + Area 3	=	Area of hemisphere +two(Area of triangle ABC)
2A + 2B + 2C	=	2 $\pi$ + 2(Surface area of triangle ABC)
Area of triangle ABC	=	A + B + C - $\pi$ .

3. Non-Euclidean Geometry

Sometimes revolutionary discoveries are goose egg more than actually seeing what has been under our noses all the fourth dimension. This was the case over the discovery of Not-Euclidean Geometry in the nineteenth century. For some 2000 years after Euclid wrote his 'Elements' in 325 BC people tried to prove the parallel postulate equally a theorem in the geometry from the other axioms merely always failed and that is a long story. Meanwhile mathematicians were using spherical geometry all the fourth dimension, a geometry which obeys the other axioms of Euclidean Geometry and contains many of the same theorems, simply in which the parallel postulate does non hold. All along they had an case of a Non-Euclidean Geometry under their noses.

Think of a line 50 and a point P not on L. The big question is: "How many lines can be drawn through P parallel to Fifty?" In Euclidean Geometry the answer is ``exactly one" and this is ane version of the parallel postulate. If the sum of the angles of every triangle in the geometry is $\pi$ radians then the parallel postulate holds and vice versa, the ii properties are equivalent.

In spherical geometry, the basic axioms which we presume (the rules of the game) are dissimilar from Euclidean Geometry - this is a Non-Euclidean Geometry. Nosotros have seen that in spherical geometry the angles of triangles practise non always add up to $\pi$ radians so we would not expect the parallel postulate to hold. In spherical geometry, the straight lines (lines of shortest distance or geodesics) are bang-up circles and every line in the geometry cuts every other line in two points. The reply to the big question most parallels is``If nosotros accept a line L and a point P non on L then there are no lines through P parallel to the line L."

The Greek mathematicians (for case Ptolemy c 150) computed the measurements of correct angled spherical triangles and worked with formulae of spherical trigonometry and Arab mathematicians (for example Jabir ibn Aflah c 1125 and Nasir ed-din c 1250) extended the work even further. The formula discussed in this article was discovered by Harriot in 1603 and published by Girard in 1629. Further ideas of the subject were developed past Saccerhi (1667 - 1733).

All this went largely un-noticed by the 19th century discoverers of hyperbolic geometry, which is another Non-Euclidean Geometry where the parallel postulate does not hold. In spherical geometry (besides called elliptic geometry) the angles of triangles add upwards to more than $\pi$ radians and in hyperbolic geometry the angles of triangles add up to less than $\pi$ radians.

For further reading see the article by Alan Beardon 'How many Geometries Are There?' and the article by Keith Carne 'Strange Geometries' . At that place are some applied activities that y'all tin endeavour for yourself to explore these geometries further to exist found at http://nrich.maths.org/MOTIVATE/conf8/alphabetize.html