4 Pi R 2 Area

Area of a Circle

The area of a circle is the infinite occupied past the circumvolve in a 2-dimensional plane. Alternatively, the space occupied within the boundary/circumference of a circle is called the expanse of the circumvolve. The formula for the expanse of a circumvolve is A = πr², where r is the radius of the circle. The unit of expanse is the square unit, for example, thou², cm^two, in^two, etc. Surface area of Circle = πr² or πd²/4 in square units, where (Pi) π = 22/7 or 3.14. Pi (π) is the ratio of circumference to bore of any circle. It is a special mathematical constant.

The area of a circumvolve formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular tabular array, then the area formula will help us to know how much textile is needed to cover it completely. The expanse formula will too aid u.s. to know the boundary length i.due east., the circumference of the circumvolve. Does a circle have book? No, a circle doesn't have a volume. A circle is a two-dimensional shape, it does not have volume. A circle simply has an surface area and perimeter/circumference. Permit united states learn in detail about the expanse of a circumvolve, surface expanse, and its circumference with examples.

1.	Circle and Parts of a Circumvolve
two.	What Is the Area of Circle?
3.	Expanse of Circle Formulas
iv.	Derivation of Area of a Circle Formula
5.	Surface area of Circle Formula
6.	Real-World Example on Area of Circle
vii.	FAQs on Area of Circumvolve

Circle and Parts of a Circumvolve

A circle is a collection of points that are at a fixed distance from the eye of the circumvolve. A circle is a closed geometric shape. We see circles in everyday life such equally a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed within the circumvolve is known as the area of the circle.

Radius: The altitude from the eye to a indicate on the boundary is called the radius of a circumvolve. It is represented by the letter 'r' or 'R'. Radius plays an of import role in the formula for the area and circumference of a circle, which we will learn afterward.

Diameter: A line that passes through the center and its endpoints prevarication on the circle is called the diameter of a circle. It is represented past the letter 'd' or 'D'.

Diameter formula: The diameter formula of a circle is twice its radius. Diameter = ii × Radius

d = 2r or D = 2R

If the diameter of a circle is known, its radius can exist calculated as:

r = d/ii or R = D/2

Circumference: The circumference of the circle is equal to the length of its boundary. This means that the perimeter of a circumvolve is equal to its circumference. The length of the rope that wraps around the circle's boundary perfectly will be equal to its circumference. The beneath-given figure helps you visualize the same. The circumference can be measured by using the given formula:

where 'r' is the radius of the circle and π is the mathematical constant whose value is approximated to 3.14 or 22/7. The circumference of a circumvolve can be used to find the area of that circle.

For a circle with radius 'r' and circumference 'C':

• π = Circumference/Bore
• π = C/2r = C/d
• C = 2πr

Permit us sympathise the dissimilar parts of a circle using the following real-life example.

Consider a circular-shaped park equally shown in the figure below. We can identify the various parts of a circle with the help of the figure and tabular array given below.

In a Circle	In our park	Named by the letter
Centre	Fountain	F
Circumference	Boundary
Chord	Play area archway	PQ
Radius	Altitude from the fountain to the Entrance gate	FA
Bore	Straight Line Distance between Archway Gate and Exit Gate through the fountain	AFB
Small segment	The smaller surface area of the park, which is shown as the Play area
Major segment	The bigger area of the park, other than the Play area
Interior part of the circle	The light-green area of the whole park
Exterior office of the circle	The expanse outside the boundary of the park
Arc	Any curved part on the circumference.

What is the Area of Circle?

The area of a circle is the amount of space enclosed within the purlieus of a circle. The region within the purlieus of the circle is the area occupied by the circle. It may also be referred to as the total number of square units within that circle.

Surface area of Circumvolve Formulas

The expanse of a circle tin can be calculated in intermediate steps from the diameter, and the circumference of a circle. From the diameter and the circumference, we can find the radius and then find the area of a circle. Simply these formulae provide the shortest method to find the area of a circle. Suppose a circumvolve has a radius 'r' then the expanse of circle = πr² or πdⁱⁱ/4 in foursquare units, where π = 22/7 or 3.14, and d is the bore.

Area of a circumvolve, A = πrⁱⁱ square units

Circumference / Perimeter = 2πr units

Area of a circumvolve can exist calculated past using the formulas:

• Expanse = π × r², where 'r' is the radius.
• Surface area = (π/4) × d², where 'd' is the bore.
• Area = C²/4π, where 'C' is the circumference.

Examples using Area of Circle Formula

Let us consider the post-obit illustrations based on the area of circle formula.

Instance 1: If the length of the radius of a circle is iv units. Calculate its expanse.

Solution:
Radius(r) = four units(given)
Using the formula for the circle'southward area,
Area of a Circle = πr²
Put the values,
A = π4²
A =π × sixteen
A = 16π ≈ 50.27

Answer: The area of the circumvolve is 50.27 squared units.

Example ii: The length of the largest chord of a circle is 12 units. Notice the surface area of the circle.

Solution:
Bore(d) = 12 units(given)
Using the formula for the circle's area,
Area of a Circle = (π/4)×dⁱⁱ
Put the values,
A = (π/four) × 12²
A = (π/4) × 144
A = 36π ≈ 113.1

Answer: The area of the circle is 113.1 square units.

Expanse of a Circle Using Diameter

The area of the circle formula in terms of the diameter is: Area of a Circle = πd²/4. Here 'd' is the diameter of the circumvolve. The diameter of the circle is twice the radius of the circle. d = 2r. Generally from the diameter, we need to offset find the radius of the circumvolve and then find the area of the circumvolve. With this formula, we can direct find the area of the circumvolve, from the measure out of the bore of the circle.

Area of a Circle Using Circumference

The expanse of a circumvolve formula in terms of the circumference is given by the formula \(\dfrac{(Circumference)^2}{4\pi}\). At that place are two simple steps to observe the surface area of a circle from the given circumference of a circumvolve. The circumference of a circumvolve is get-go used to find the radius of the circle. This radius is farther helpful to observe the area of a circumvolve. But in this formulae, we will be able to directly notice the area of a circle from the circumference of the circle.

Expanse of a Circumvolve-Calculation

The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the surface area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14. Any of the values of pi can exist used based on the requirement and the need of the equations. The beneath table shows the list of formulae if nosotros know the radius, the diameter, or the circumference of a circle.

Surface area of a circle when the radius is known.	πr2
Area of a circle when the diameter is known.	πd2/four
Expanse of a circle when the circumference is known.	C two/4π

Derivation of Expanse of a Circle

Why is the area of the circle is πr²? To empathize this, let'southward get-go sympathize how the formula for the area of a circle is derived.

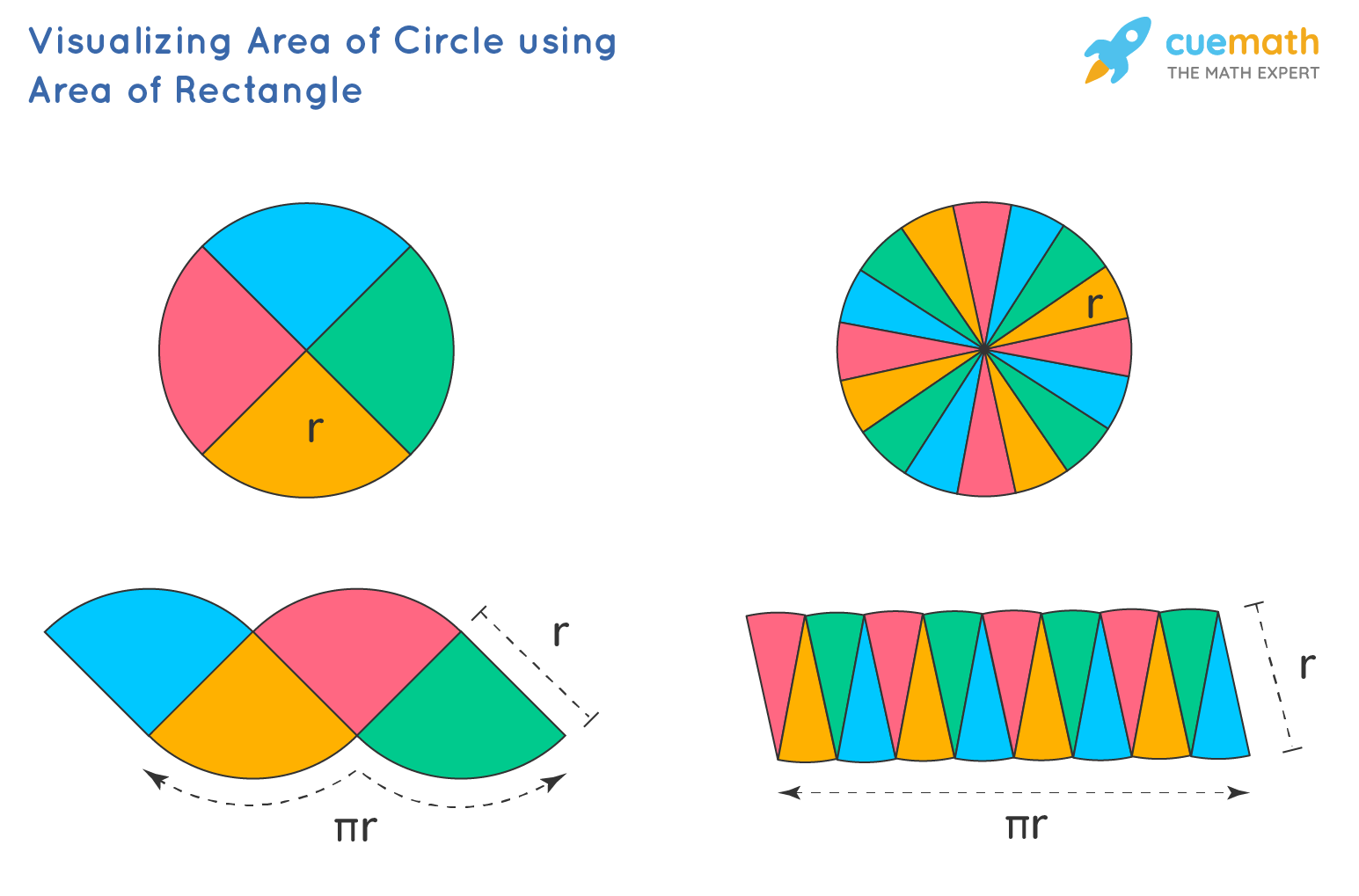
Observe the above figure carefully, if we split up the circumvolve into smaller sections and arrange them systematically it forms a shape of a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. The more than the number of sections it has more it tends to have a shape of a rectangle every bit shown to a higher place.

The expanse of a rectangle is = length × breadth

The latitude of a rectangle = radius of a circle (r)

When nosotros compare the length of a rectangle and the circumference of a circumvolve we can see that the length is = ½ the circumference of a circle

Area of circle = Surface area of rectangle formed = ½ (2πr) × r

Therefore, the expanse of the circle is πr², where r, is the radius of the circumvolve and the value of π is 22/vii or 3.14.

Surface Expanse of Circle Formula

The surface area of a circumvolve is the same as the expanse of a circle. In fact, when we say the area of a circle, we mean zippo only its total surface surface area. Surface surface area is the expanse occupied past the surface of a iii-D shape. The surface of a sphere will be spherical in shape only a circumvolve is a simple plane two-dimensional shape.

If the length of the radius or bore or even the circumference of the circle is given, and so nosotros can find out the surface area. It is represented in square units. The surface area of circle formula = πr^two where 'r' is the radius of the circle and the value of π is approximately 3.14 or 22/seven.

Real-World Instance on Expanse of Circle

Ron and his friends ordered a pizza on Friday dark. Each slice was fifteen cm in length.

Calculate the area of the pizza that was ordered by Ron. You can assume that the length of the pizza piece is equal to the pizza's radius.

Solution:

A pizza is circular in shape. So we can use the area of a circle formula to calculate the area of the pizza.

Radius is 15 cm

Expanse of Circle formula = πr² = 3.xiv × 15 × fifteen = 706.five

Expanse of the Pizza = 706.5 sq. cm.

Area of Circle Examples

1. Example 1: Observe the circumference and the surface area of a circle whose radius is 14 cm.

   Solution:

   Given: Radius of the circumvolve = 14 cm

   Circumference of the Circle = 2πr

   = 2 × 22/vii × 14

   = 2 × 22 × 2

   = 88 cm

   Using area of Circle formula = πr²

   = 22/7 × 14 × 14

   = 22 × 2 × xiv

   = 616 sq. cm.

   Area of the Circumvolve = 616 sq. cm.

2. Instance 2: The ratio of the surface area of 2 circles is 4:9. With the help of the surface area of circle formula find the ratio of their radii.

   Solution:

   Let us presume the post-obit:

   The radius of the 1st circle = R1

   Area of the 1st circle = A1

   The radius of the 2nd circle = R2

   Area of the 2nd circle = A2

   Information technology is given that A1:A2 = 4:ix

   Surface area of a Circle = πrⁱⁱ

   π\(R_1\)ⁱⁱ : π\(R_2\)² = 4 : 9

   Taking square roots of both sides,

   R1 : R2 = two : 3

   Therefore, the ratio of the radii = 2:three

3. Example 3: A race track is in the form of a round ring. The inner radius of the rail is 58 yd and the outer radius is 63 yd. Find the surface area of the race rails.

   Solution:

   Given: R = 63 yd, r = 56 yd.

   Allow the area of outer circumvolve be A₁ and the area of inner circle be A_ii

   Area of race track = A₁ - A₂ = πR^two - πr² = π(63² - 56²) = 22/7 × 833 = ii,618 square yards.

   Therefore, the area of the race rails is 2618 square yards.

4. Example 4: A wire is in the shape of an equilateral triangle. Each side of the triangle measures 7 in. The wire is bent into the shape of a circle. Find the area of the circle that is formed.

   Solution:

   Perimeter of the Equilateral Triangle: Perimeter of the triangle = three × side = 3 × 7 = 21 inches.

   Since the perimeter of the equilateral triangle = Circumference of the circle formed.

   Thus, the perimeter of the triangle is 21 inches.

   Circumference of a Circle = 2πr = 2 × 22/seven × r = 21. r = (21 × 7)/(44) = 3.34.

   Therefore, the Radius of the circumvolve is 3.34 cm. Area of a circle = πr² = 22/7 ×(three.34)² = 35.042 square inches.

   Therefore, the surface area of a circle is 35.042 square inches.

5. Example five: The time shown in a round clock is iii:00 pm. The length of the minute hand is 21 units. Find the distance traveled by the tip of the minute mitt when the fourth dimension is iii:30 pm.

   Solution:

   When the minute hand is at 3:30 pm, information technology covers half of the circle. Then, the altitude traveled by the infinitesimal paw is actually one-half of the circumference. Altitude \(= \pi\) (where r is the length of the minute hand). Hence the distance covered = 22/7 × 21 = 22 × 3 = 66 units. Therefore, the altitude traveled is 66 units.

get to slidego to slidego to slidego to slidego to slide

Have your child solve real-life challenges using math

Have your child apply concepts learned in school in the real world with the help of our experts.

Book a Free Trial Course

Practise Questions on Expanse of Circumvolve

go to slidego to slide

FAQs on Area of Circle

How to Calculate the Area of a Circle?

The area of circle is calculated by using the following listed formulas:

• Area = π × r^two, where 'r' is the radius.
• Area = (π/4) × d², where 'd' is the diameter.
• Area = C^two/4π, where 'C' is the circumference.

What Is the Area of Circle Formula?

Area of circumvolve formula = π × r². The area of a circle is π multiplied by the square of the radius. The expanse of a circle when the radius 'r' is given is πr². The area of a circle when the bore 'd' is known is πdⁱⁱ/four. π is approx 3.14 or 22/vii. Area(A) could also be found using the formulas A = (π/four) × d², where 'd' is the radius and A= C²/4π, where 'C' is the given circumference.

What Is the Perimeter and Expanse of a Circle?

The circumference of the circle is equal to the length of its boundary. This means that the perimeter of a circle is equal to its circumference. The expanse of a circle is πr² and the perimeter (circumference) is 2πr when the radius is 'r' units, π is approx iii.14 or 22/7. The circumference and the radius length of a circle are of import parameters to discover the area of that circle. For a circumvolve with radius 'r' and circumference 'C':

• π = Circumference ÷ Diameter
• π = C/2r
• Therefore, C = 2πr

Why Is the Area of a Circle Formula is πr²?

A circle tin can be divided into many small sectors which tin so exist rearranged appropriately to grade a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle. Nosotros can clearly see that one of the sides of the rectangle will be the radius and the other will be one-half the length of the circumference, i.eastward, π. Every bit we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'. Therefore, the area of the circumvolve is πrⁱⁱ.

What Is the Surface area of a Circle Formula in Terms of π?

The value of pi (π) is approximately 3.xiv. Pi is an irrational number. This means that its decimal class neither ends (like one/5 = 0.ii) nor becomes repetitive (similar 1/3 = 0.3333...). Pi is 3.141592653589793238... (to only 18 decimal places). Hence the expanse of a circle formula in terms of pi is given as πrⁱⁱ foursquare units.

How Do You Notice the Circumference and Expanse of a Circle?

The area and circumference of a circumvolve can be calculated using the following formulas. Circumference = 2πr ; Area = πr². The circumference of the circle tin can be taken as π times the diameter of the circumvolve. And the area of the circumvolve is π times the square of the radius of the circle.

How to Calculate the Area of a Circle With Bore?

The diameter of the circle is double the radius of the circle. Hence the area of the circle formula using the diameter is equal to π/4 times the square of the diameter of the circle. The formula for the surface area of the circle, using the diameter of the circle π/4 × diameter^two.

How Practise You Find the Expanse of a Circle Given the Circumference?

The area of a circle tin also exist plant using the circumference of the circle. The radius of the circle can be establish from the circumference of the circle and this value tin can be used to find the area of the circle. Assume that the circumference of the circle is 'C'. We accept C = 2πr, or r = C/2π. At present applying this 'C' value in the Area formula we have A = πr² = π × (C/2π)² = C²/4π.

What Is the Area of Circle With Radius 3 m?

The area of a circumvolve is π multiplied by the square of the radius. The surface area of a circumvolve(A) when the radius 'r' is given is πr². π is approx iii.14 or 22/7. Therefore, area = 3.14 × iii × three = 28.26 sq. m.

The Circumference of a Given Circle Is sixteen cm. What Will Be Its Area?

Circumference of a circumvolve = xvi cm

We know the formula of circumference, C =2πr
And so,
2πr = 16
or r = 16/2π = eight/π
Substituting the value of 'r' in the area of circumvolve formula, we go:
A = πr²
A = π(8/π)^two = 64/π
On solving,
Area = xx.38 sq. cm.

4 Pi R 2 Area,

Source: https://www.cuemath.com/geometry/area-of-a-circle/

Posted by: sosaammed1971.blogspot.com

Share this post